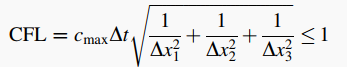叠合层的刚度矩阵

当波沿着正交各向异性板主轴传播时，刚度矩阵可为：

使用变换矩阵处理：

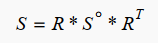
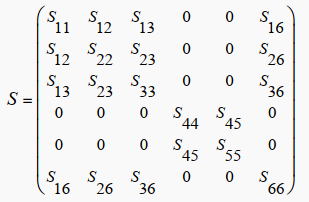
其中变换矩阵为：

叠合层的粘度矩阵

引入粘度矩阵来描述阻尼

和刚度矩阵的情况类似，一旦堆叠方向不在坐标轴方向，就需要对粘度矩阵进行处理：

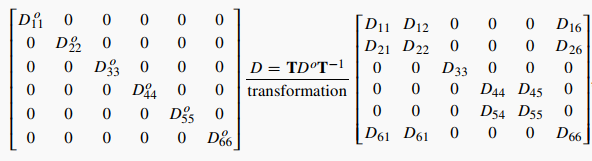
旋转矩阵为：

总的位移值可以拆分为刚度部分和阻尼部分的和，最终的有限差分法在阻尼部分的迭代方程可见点此跳转文献链接

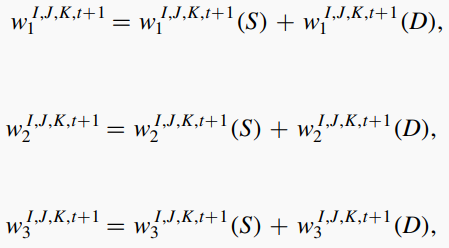
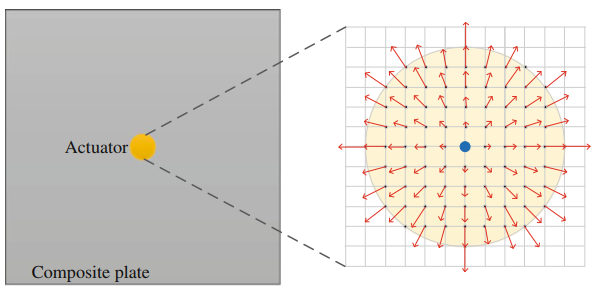
压电传感器和结构的耦合作用

使用ANSYS对PZT传感器以及一小片带有无反射边界（NRB）叠合板进行建模，并通过 frequency domain harmonic analysis获得频域响应（位移）：

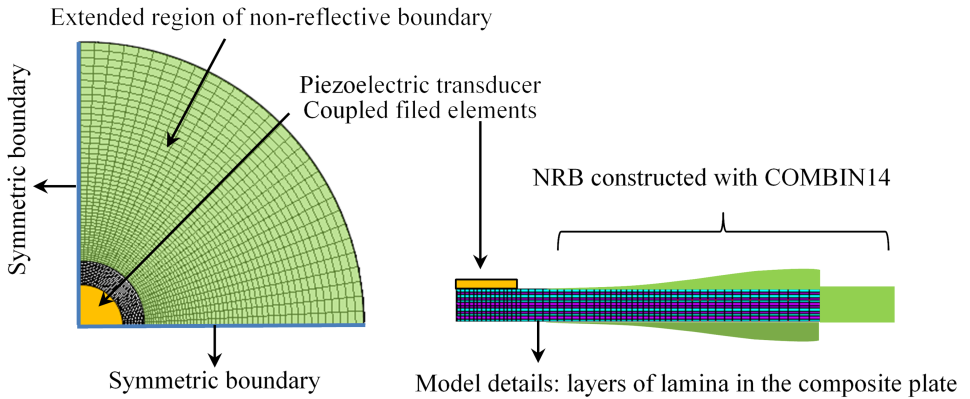
记频域响应为：

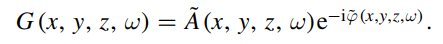
对实际激励信号进行傅里叶变换并记为 $\tilde{V}(\omega)$ ，则叠合板处在频域上的响应为：

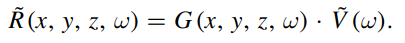
通过逆变换可得叠合板上由PZT板激励的实际位移：

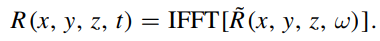
对于各向异性板，导波的传播方程为：

在对上式下标进行简化后，可以写为：

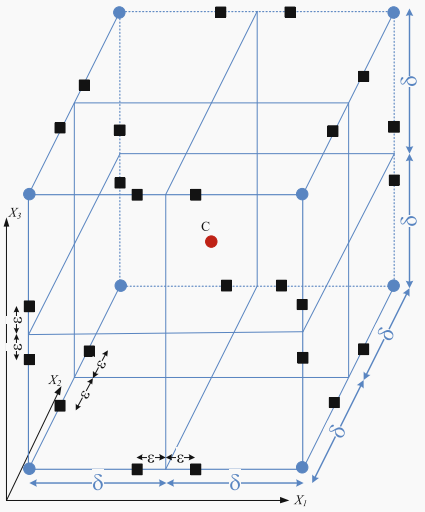
将板结构进行离散化，下方右图中的 $\delta$ 是用来表征立方体中心点在哪一侧的导数。

则中心单元的二阶偏导有：

其中：

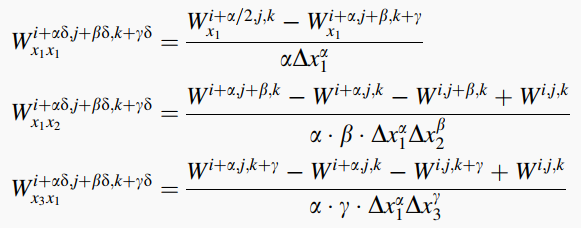
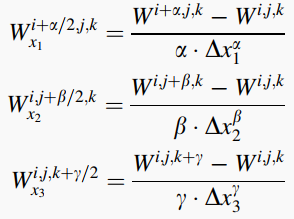
对应原先边长为 $\delta$ 的小立方体的边界的的一阶偏导有：

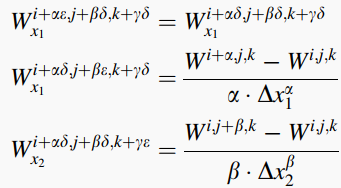
通过下式可将上式中的位移分量转化为应力分量：

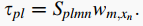
从而可以使用上中心点处的剪应力连续条件：

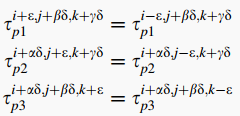
其中， $\rho=1,2,3$ 。

最终的三个位移分量的有限差分法迭代方程可见（太长了）：
点此跳转文献链接

此外，应当满足约束：